Más de 300 mil personas rindieron la Prueba de Admisión a la Educación Superior (PAES) Regular 2026, instancia que les permitirá postular a las 47 universidades adscritas al sistema de acceso a la educación superior.
El Departamento de Evaluación, Medición y Registro Educacional (Demre) destacó que se trata de la cifra más alta de inscritos en la historia, para quienes se habilitaron 203 sedes de rendición a lo largo de Chile, incorporándose este año Bulnes (Región de Ñuble) y Cunco (La Araucanía).
Dentro de las cuatro pruebas a rendir, entre ellas Matemática 1, Matemáticas 2, Ciencias, Historia y Ciencias Sociales y sus cientos de preguntas, hubo una que no pasó desapercibida.
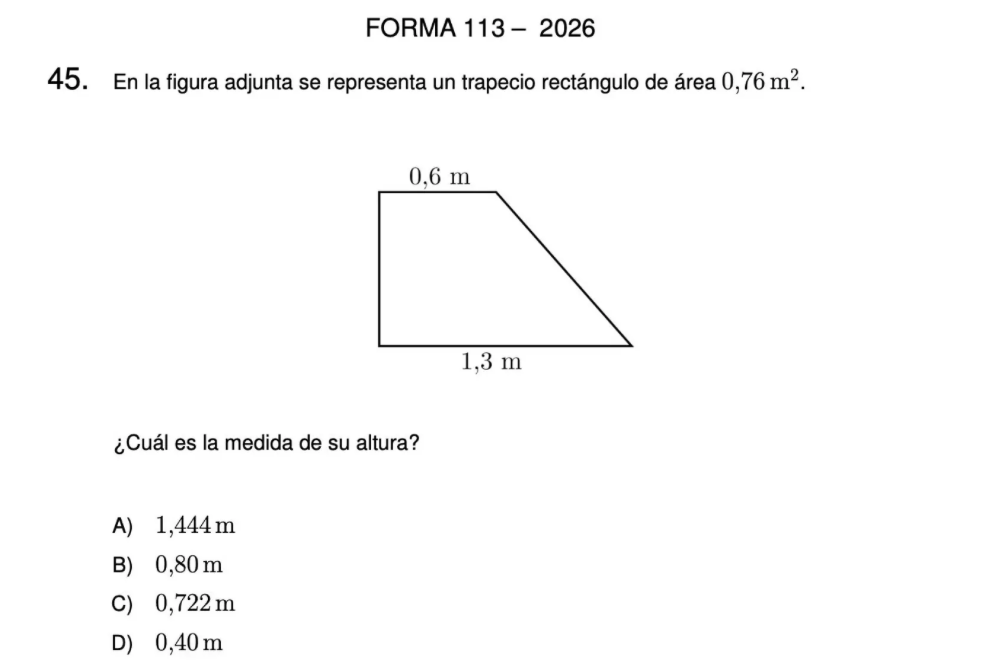
Se trata de un ejercicio de un trapecio rectángulo, es decir, que uno de sus lados no paralelos es perfectamente vertical. En la pregunta hay tres datos: las dos longitudes de las bases y el área total en metros cuadrados. La resolución es calcular la altura del trapecio y para ello hay cuatro alternativas de respuesta.
Según Rodrigo Orellana, estudiante del plan común de Ingeniería de la U. de Chile reveló que el problema "es difícil para ser la PAES", consignó a LUN. En esa línea, Mabel Vega, doctora en Educación e Investigación, magíster en Didáctica de la Matemática y Académica de la Universidad Mayor señaló que "exige despejar una variable, lo cual implica manejo algebraico básico y compresión de operaciones con decimales".
PASOS PARA RESOLVER EL EJERCICIO
- Identificar los datos: la base mayor mide 1,3 metros, la base menor mide 0,6 metros y el área del trapecio es 0.76 metros cuadrados.
- El segundo paso es aplicar la fórmula: El área de un trapecio se calcula como la suma de sus bases, dividido en 2 y multiplicado por la altura.
- Luego, se deben sumar las bases 1,3 m + 0,6 = 1,9 m.
- Sustituir los valores con la fórmula. Es decir, 0,76 metros cuadrados (área) = 1,9 metros x altura (h) dividido por 2.
- Despejar la altura, para eso las cifras 2 y 19 pasan al otro lado del =, pero cambiando la operación: es decir, si a la derecha el 2 divide, a la izquierda multiplica, en tanto el 1,9 m pasa de multiplicar a la derecha a dividir a la izquierda.
- Para eso hay que multiplicar 0,76 x 2 (1.52) y dividirlo por 1,9.
- El resultado es 0,8 metros.
- Por ende, la respuesta correcta es la B.




